Archived Pages
- Initial (2009) Proposal
Initial (2009) Proposal
download this document in PDF form
University of Texas GeoFluids Consortium (UT GeoFluids):
Mudrock Geomechanics & Pore Pressure Prediction
Description & Objectives1.0 Executive Summary
Overview: UT GeoFluids will study the state and evolution of pressure, stress, deformation and fluid migration through experiments, theoretical analysis, and field study. The Bureau of Economic Geology (BEG) at the Jackson School of Geosciences will partner with the Department of Civil and Environmental Engineering at MIT: BEG will lead the consortium.
Experimental: We will analyze the fabric, acoustic, electrical, and mechanical properties of mudrocks over effective stresses from 0.1-100 MPa. We will study 1) real geologic materials (Gulf of Mexico mudrock, Boston Blue Clay) using resedimentation techniques and 2) core from a range of depths in the subsurface. Analysis of resedimented material allows us to examine material properties of a consistent material at a range of in-situ stresses. Uniaxial consolidation experiments will measure vertical and lateral stress, resistivity, permeability, and velocity (Vp & Vs) during compression. Triaxial experiments will measure strength parameters. We will describe and quantify mudrock fabric at various effective stresses with mercury porosimetry, and x-ray goniometry and image mudrock fabric using electron beam techniques. We will 1) illuminate the origin and evolution anisotropy in mudrocks, 2) document how composition (e.g. clay/silt fraction and clay composition) controls geomechanical properties, and 3) develop a geomechanical model for mudrocks that will better allow us to predict compaction behavior, pore pressure, and borehole stability at geologic stresses.
Poro-Mechanical Modeling: We will develop and apply models that link realistic rheologies, deformation, stress (shear and normal), and pore pressure. Pressure prediction techniques and basin modeling generally assume uniaxial deformation. In areas of central interest to the petroleum industry, deformation is not uniaxial and stress and pressure are coupled in more complex ways. In thrust belts, the lateral stress is greater than the vertical stress and sediment that was originally buried in a basin under uniaxial strain is later deformed in plane strain. In the sub-salt regime, the interaction of isostatically stressed salt with sediment that bears differential stresses results in complex stress and deformation near the salt-sediment interface. To understand and ultimately predict pressures, stresses, and rock properties in these regimes, a new level of understanding, modeling, and analysis must be applied.Field Study: We will analysize pore pressure in thrust belts and in salt provinces. In the subsalt, we will analyze pressure and stress in and near the Mad Dog field to understand how pore pressure couples with salt advancement and to study the present state of stress and pressure in sub-salt systems. We will study fold thrust systems through ongoing work in the Nankai Trough. We look forward to working with industry data sets in deepwater fold-thrust belts.
Importance: Despite extensive previous work exploring mudrock compressional behavior, there are still major gaps in our understanding of mudrock evolution. We do not yet have an understanding of stress and strength behavior over a large range of effective stresses (0.1-100 MPa) and we do not fully understand the evolution of anisotropy. Our work will lay the groundwork for a new generation of basin modeling algorithms and pressure/stress prediction techniques. This new generation of modeling techniques will go beyond the restrictive assumption that deformation is uniaxial. Instead, we will couple reasonable assumptions about far field stress state with rheological models to predict stress and pressure. The results will allow us to better predict pressure, stress, borehole stability, and hydrocarbon migration in environments critical to exploration: thrust belts and sub-salt.
Reporting: The Consortium will 1) hold Annual Meetings, 2) provide Annual Reports, 3) develop an on-line database of experimental results, 4) provide Company Visits, and 5) provide Notice of Papers Submitted for Publication.
Research Team: The Consortium Team will include Peter Flemings (University of Texas at Austin), Ruarri Day-Stirrat (University of Texas at Austin), John Germaine (Massachusetts Institute of Technology), and Derek Elsworth (Pennsylvania State University). We envision supporting 10 graduate students and 3 post-doctoral scientists at 3 universities.
How Much?
Start Date: June 1, 2009
Duration: 10 years
Cost: $45,000/year
Project Director: Peter B. Flemings, Geoscientist and Professor
512-475-8738 (w)
2.0 UT GEOFLUIDS PLAN:
Pressure prediction techniques and basin models generally assume uniaxial deformation (Figure 1A). Pressure is predicted from a single effective stress-porosity relationship (Figure 1B,C) and the least principal effective stress (fracture gradient) is modeled as a fraction the vertical effective stress (parameterized by the stress ratio, Ko) (Figure 1C).
In practice, the specific nature of the porosity-effective stress relationship and the effective stress ratio (Ko) are empirically derived, have significant variation, and we do not understand well what controls this variability. At geologic stresses (0.1 -100 MPa) we do not have a clear understanding of compaction or strength behavior. We do not fully understood how the fabric of a compacting mud rock evolves. Thus, the evolution of anisotropy (strength, permeability, resistivity, velocity) is poorly undertood.
Figure 1: A) Uniaxial strain is generally assumed in pressure predictiona and basin modeling. B) Under these conditions, there is a single relationship between vertical effective stress and strain. D) In complex stress regimes, vertical and lateral strain occurs. E) Here, the rock that is subject to both vertical and lateral shortening behaves more stiffly (red dashed line) than the same rock undergoing uniaxial strain (solid black line). F) Predicted pore pressures are lower, yet horizontal stresses are higher in this example relative to the uniaxial strain example.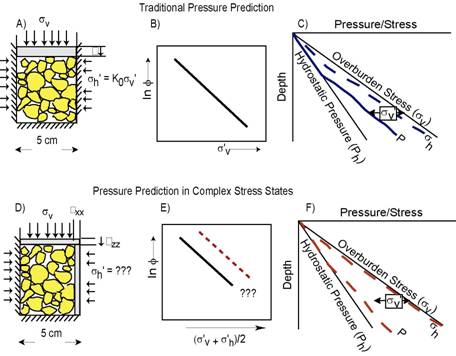
In settings of critical interest to industry, strain is not uniaxial. Under these conditions, the porosity-effective stress relationship will be different (red dashed line vs. solid black line, Fig 1E). There has been little effort to incorporate this behavior in the study of mudrock consolidation. We illustrate that rocks with the same observed porosity will have different pressures because one region was subject to uniaxial strain (top) whereas the other has both vertical and lateral strain imposed (bottom) (Figure 1).
The example above illustrates the importance of this problem for predicting pressure. However, the problem also applies to basin modeling. Most basin modeling software assumes uniaxial strain (e.g. IFP’s Temispack, IES’s Petromod, or our own (Dugan, 2000). By definition these modeling packages cannot capture the physical processes that occur when strain is not uniaxial. As a result they will incorrectly simulate pore pressures and resultant flow and they cannot capture variations in the stress field.
This consortium will pursue three directions. 1) We will perform a broad range of experimental measurements to analyze the evolution of mudrocks through mechanical compaction. 2) We will develop geological models that incorporate a full soil model and thus the effects of both mean and shear stress: we will be able to predict both stress and pressure. 3) We will pursue field studies in two environments where the uniaxial strain assumption is not appropriate: salt environments and fold-thrust environments. The goal is to develop, through analysis of data sets and theoretical modeling, a fundamental understanding of the evolution of pressure, stress, and rock properties in these systems. From this understanding we will develop specific pressure prediction and basin modeling techniques that will be broadly applicable.
2.1 Mudrock Properties: Experimental Program
Overview:
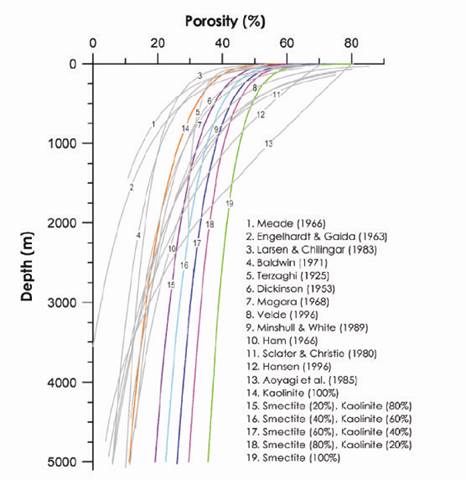
There are a wide range of porosity-effective stress relationships that have been developed (Figure 2). Burland et al. (1990) summarized the dependency of compression behavior on clay content. Karig and Hou (1992) used mixtures of material to illustrated striking differences in compression behavior between mudstones and sandstones. Fukue et al. (1986) explored the variation in compressibility for a range of clay-silt mixtures. Aplin and Yang (1995) used well cuttings to illustrate how compression behavior varies with clay content. Dewhurst and Aplin (1998, 1999) experimentally examined the evolution of permeability, porosity, specific surface area, and pore throat distribution within mudstones and siltstones of London Clay mudstone. Yang and Aplin (2004) presented compressibility behavior of well data emphasizing the importance of clay content on compressibility. Most recently, Mondol et al. (2007) described the compression and velocity behavior of synthetic mixtures ranging from pure smectite to pure kaolinite.
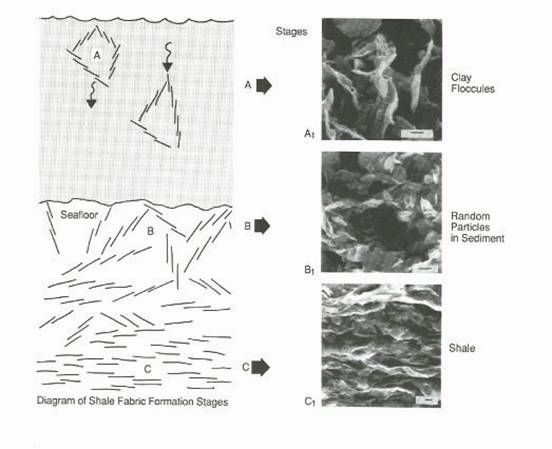
Figure 2: Illustration of the many porosity vs. depth relationships for mudrocks (Mondol et al., 2007).There are still major gaps in our understanding of the evolution of mudrocks. We do not yet have a predictive understanding of stress and strength behavior over a large range of effective stresses (0.1-100 MPa). How does anisotropy evolve in mud rock successions? Kwon et al. (Kwon et al., 2004a; Kwon et al., 2004b) demonstrate permeability anisotropy in Gulf Coast Wilcox formation samples at 4km, but the question of when and how anisotropy develops remains (Figure 3).
Figure 3: Shale fabric changes during consolidation. (O'Brien and Slatt, 1990).
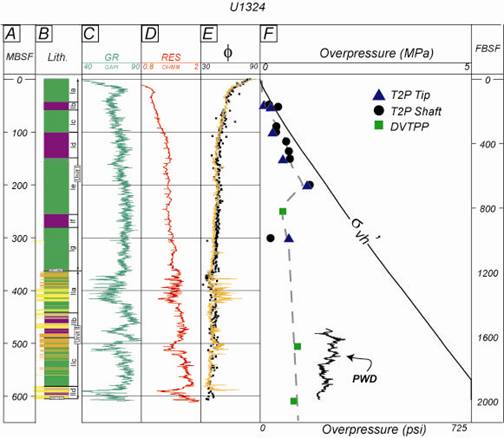
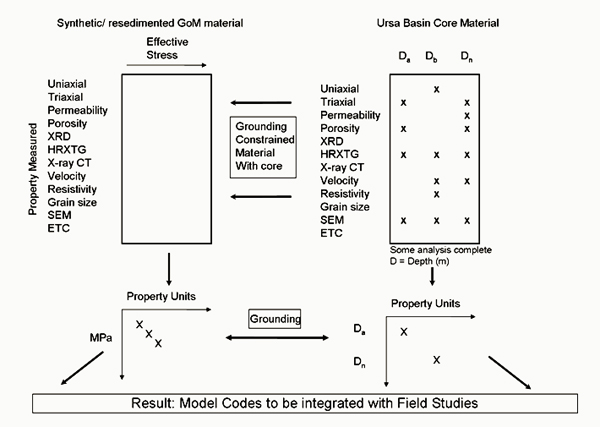
We will analyze the fabric, acoustic, electrical, and material properties of mudrocks over effective stresses from 0.1-100 MPa. We will study 1) synthetic mixtures and real geologic materials (Gulf of Mexico mudrock) using resedimentation techniques and 2) intact cores from a range of in-situ effective stresses (Ursa Region, Figure 4). We will use these materials to study the evolution of mudrocks during consolidation. We will use mercury injection porosimetry, X-ray diffraction, and Scanning Electron Microscopy and high resolution X-ray texture goniometry to characterize the evolution of pore throat geometry, quantify composition and clay fabric intensity, and provide images. We will characterize permeability, and compressibility. Analysis of resedimented material will allow us to examine material properties of a consistent material at a range of in-situ stresses. Uniaxial consolidation experiments will measure vertical and lateral stress, resistivity, permeability, and velocity (Vp & Vs) (Figure 5). Triaxial experiments will measure strength parameters. The experimental suite will be grounded and augmented by extensive whole cores from 0-600 meters below mudline in the Ursa Region of the Gulf of Mexico (Figure 5). These cores are largely composed of mudrock of a relatively homogenous composition that have been consolidated from a surface porosity of approximately 70% to a minimum porosity of 35% at a depth of 600 mbsf.
Figure 4: Hole U1324 from the Ursa Basin, Gulf of Mexico (Flemings et al., 2008). A broad range of data including intact core, logging data, and other physical property data are available.
The primary goal of the experimental program is to provide the underpinnings for more complex and comprehensive mudrock models than are currently used in the energy industry. Through this analysis we will 1) illuminate the origin and evolution of anisotropy in mudrocks, 2) illuminate how composition (e.g. clay/silt fraction and clay composition) impacts geomechanical properties, and 3) develop a geomechanical model for mudrocks that will better allow us to predict compaction behavior, pore pressure, and borehole stability at geologic stresses (Figure 5).
The long term motivation is to:
- Improve geophysical imaging by having a better understanding of propagation velocity, elastic anisotropy, and resistivity anisotropy as a function of mudrock density.
- Design drilling programs by having a better understanding of the stress profile and mechanical properties of the mudrock.
- Provide parameters for forward modeling of basin evolution
- Develop tools to predict pore pressure and stress from rock properties
We will measure the following parameters:
1. Velocity: vertical compressional (Vp) and Shear (Vs) velocity at various stress levels during uniaxial consolidation.
2. Stress (horizontal and vertical) and undrained compression strength will be measured by triaxial measurements at various stages of consolidation.
3. Resistivity: Vertical and horizontal resistivity will be measured at various stress levels during uniaxial compression.
4. Permeability: vertical permeability will be measured as a continuous function of compression. Horizontal permeability will be measured at multiple stages of the experiment.
5. Fabric: At multiple stages of the deformation, samples will be extracted from the experimental cell and analyzed for pore structure, clay alignment, etc.
Figure 5: A full suite of experiments will be run on resedimented material (upper left). These experiments will lead to a detailed understanding of material behavior for each property over a range of stresses (lower left). In turn, measurements will be made on intact core (upper right). We will compare results from resedimented material (left side) to results from intact core (right side) and from this analysis develop a broad model of behavior of intact mudstone (lower right).
2.2 Coupled Poromechanical Modeling:
We will develop and apply coupled poromechanical models of sedimentary basin evolution. This type of modeling is used routinely in the geotechnical community. We envision two approaches; 1) we will use static stress modeling to expore the present day state of stress and pressure in meaningful geological scenarios; and 2) we will use coupled poromechanical models to describe the evolution of geological systems.
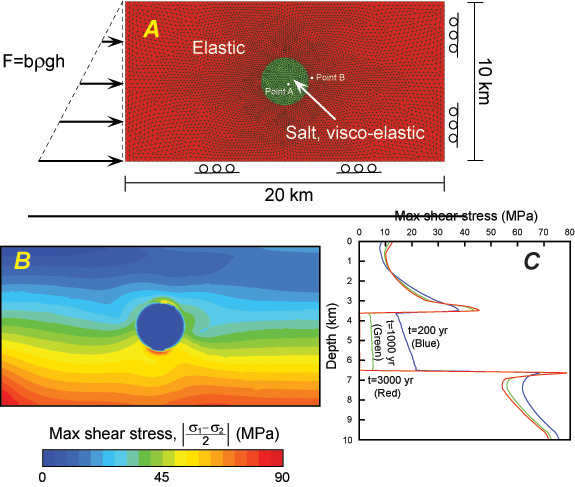
A static stress model is shown below. We have reproduced results presented by Fredrich et al (Fredrich et al., 2003) to illustrate the approach (Figure 6). We assume visco-elastic salt behavior and elastic soil behavior. The necessity for both isostatic stresses in the salt and continuity of deformations at the salt/formation interface can induce stress perturbations and stress rotations in the near-salt formations (Figure 6) (Fredrich et al., 2003; Rohleder et al., 2003). We observe signficant stress concentrations at the top and base of the salt body (Figure 6, bottom Left). Large differences in stresses can be generated that, if sufficient, induce shear failure of the formation near salt. This approach provides fascinating insight into several important issues including: 1) how to estimate vertical stress in salt systems; 2) the behavior of least principal stress at the salt-sediment interface; 3) where high shear is encountered and failure might be expected.
We will further this approach in the following ways. First we will consider realistic geometries as encountered in the case studies that we will purse (see Section 3.3). Second, we will incorporate a more realistic rock rheology into the model. We will most likely start with a Cam Clay soil model to simulate the in-situ stress state. This step is a significant one as during the relaxation process, there may be significant inelastic strains. Finally, we will couple fluid flow and stress behavior in the static stress models.
Figure 6. A: Two dimensional static stress model of circular salt body encased in elastic solid. Gravity (rgh)is included as body force. Salt is assumed to be viscoelastic (E=30GPa, v= 0.25,m= 1e19 PaS) and sediment is assumed to behave elastically (E=30GPa, v= 0.25). Boundary conditions: lateral stress increases linearly from 0 on the surface by the equation F=brgh: b is assumed to equal 0.7 to simulate a passive margin. B: maximum shear stress. Stress concentration occurs in the surrounding sediments on top and beneath the salt. C: evolution of differential shear stress along a centerline through the salt sphere during relaxation. Shear stresses in the salt gradually disappear during the processes of viscous stress relaxation.
Our second step in poromechanical modeling will be to simulate the evolution of geological systems. At the broadest level, we will incorporate stress modeling within basin modeling codes. Thus, we will go beyond current basin models (e.g. Petromod or Temis) to models that calculate stress, and deformation beyond uniaxial. We will work with the Applied Geophysics Laboratory in this development and we present one example of previous work done by AGL.
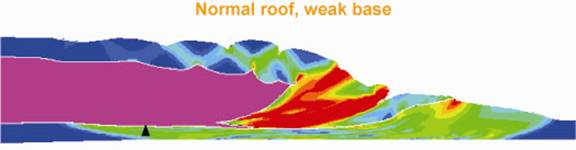
In Figure 7, a salt sheet has advanced over the underlying material. The result is concentrated zones of shear in front of the salt body. The models will require significant complexity. In particular, we envision significant problems of re-gridding around zones of large displacement.
Figure 7: Finite Element model of salt sheet advance by Dan Schultz-Ela and provided courtesy of the AGL (http://www.beg.utexas.edu/indassoc/agl/agl_if.html). Finite-element models suggest that basal shear is facilitated by very weak (overpressured) subsalt sediments. The structural style of the sheet toe may therefore be providing an indication of pressure conditions beneath the sheet. Weak sediments also permit subsalt deformation, including a footwall wedge..