Sheath Folds in Simple Shear:
An Analytical and Experimental Approach
By:
Jacqueline Reber
UTIG
| When: | Friday, September 6, 2013, 10:30 a.m. to 11:30 a.m. Join us for coffee beginning at 10:00 a.m. |
| Where: | Seminar Conference Room, 10100 Burnet Road, Bldg 196-ROC, Austin, Texas 78758 |
| Host: | Nick Hayman, UTIG |
Click for a Live Broadcast.
Abstract
Sheath folds are peculiar looking folds with a complex three-dimensional shape resembling a cone. These folds occur in many different rock types and are often associated with shear zones. They are considered a potential source of information for a kinematic and mechanical interpretation of shear zones.
Even though sheath folds have been used to infer strain magnitude, bulk strain, and shear sense in shear zones, little is known about the relation between the cause of the fold, the amount of strain, the bulk strain, and the resulting shape of the fold.
We investigate the formation and evolution of sheath folds in simple shear to obtain a better understanding of how the initial configurations, leading to the fold, manifest themselves in the resulting fold shape, and ultimately, how reliable the information obtained from sheath folds are. With a combined analytical and experimental approach, a new formation mechanism for sheath fold formation is tested and a wide parameter space investigated. We then compare the results from the analytical and experimental study with natural examples. Our study shows that sheath folds, though magnificent structures cannot be unequivocally linked to strain magnitude or bulk strain and should not be used as kinematic indicators.
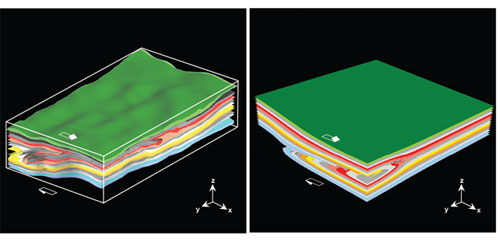
Left: Three-dimensional reconstruction (gOcad) of a sheath fold evolving around a slip surface in a silicone model. The sheath fold dips downwards into the matrix. The white arrow indicates the shear direction. Right: Three-dimensional visualization of an analytical model where the fold develops around a weak inclusion. The model is based on an adapted external Eshelby solution.




