

Next: 3. Power spectra plots
Up: 2. Models
Previous: 2.3 Mean tomography models
- rum:
- Our spherical harmonic expansion of slabs in
the upper mantle obtained from the RUM seismicity contours
[ Gudmundsson and Sambridge, 1998] which are in turn based on the
Engdahl et al. [1998] catalog. We integrate along the RUM contours at
each layer using them as
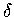 -functions such that the effective
width of the slabs is determined by
-functions such that the effective
width of the slabs is determined by
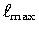 and the
and the
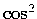 -taper that we apply for
-taper that we apply for
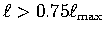 .
.
- lrr98d:
- Density model by Lithgow-Bertelloni and Richards [1998] on
spherical harmonics laterally (
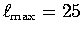 ) and layers
with depth. lrr98d is based on ``slablets'',
i.e. negative buoyancy anomalies, that sink at different
speeds in the upper and lower mantle after starting at estimated
past trench locations which are based on Mesozoic and Cenozoic plate
reconstructions [ Ricard et al., 1993; Lithgow-Bertelloni et al., 1993]. The sinking rate was
adjusted to fit geopotential fields, tomography, and plate motions.
) and layers
with depth. lrr98d is based on ``slablets'',
i.e. negative buoyancy anomalies, that sink at different
speeds in the upper and lower mantle after starting at estimated
past trench locations which are based on Mesozoic and Cenozoic plate
reconstructions [ Ricard et al., 1993; Lithgow-Bertelloni et al., 1993]. The sinking rate was
adjusted to fit geopotential fields, tomography, and plate motions.
- stb00d:
- Density model by Steinberger [2000] on
spherical harmonics (
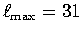 ) and radial layers.
stb00d is also based on past plate motions and
subduction; Lithgow-Bertelloni et al.'s [1993] sets of
plate boundaries were, however, interpolated at 2 Ma intervals while
Lithgow-Bertelloni and Richards [1998] held boundaries fixed during individual
plate-tectonic stages. stb00d is furthermore
different from lrr98d in that it allows for lateral
advection of slablets once they are below 380 km, due to the flow
that is generated by plate motion and slab buoyancy.
stb00d can be considered more realistic than
lrr98d with respect to the treatment of convective
flow.
) and radial layers.
stb00d is also based on past plate motions and
subduction; Lithgow-Bertelloni et al.'s [1993] sets of
plate boundaries were, however, interpolated at 2 Ma intervals while
Lithgow-Bertelloni and Richards [1998] held boundaries fixed during individual
plate-tectonic stages. stb00d is furthermore
different from lrr98d in that it allows for lateral
advection of slablets once they are below 380 km, due to the flow
that is generated by plate motion and slab buoyancy.
stb00d can be considered more realistic than
lrr98d with respect to the treatment of convective
flow.
- zmg00t:
- Temperature snapshot from a 3-D spherical
convection calculation by Zhong et al. [2000]. We use the residual (RMS)
temperature from their case 7 at time
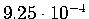 . Case 7 is
an incompressible, temperature and depth-dependent viscosity
calculation without phase transitions that allowed for plate-like
flow through the inclusion
of fixed weak zones [plates 2a and b of Zhong et al., 2000]. Assuming
constant thermal expansivity,
. Case 7 is
an incompressible, temperature and depth-dependent viscosity
calculation without phase transitions that allowed for plate-like
flow through the inclusion
of fixed weak zones [plates 2a and b of Zhong et al., 2000]. Assuming
constant thermal expansivity, 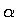 , variations in
non-dimensional temperature,
, variations in
non-dimensional temperature, 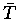 , relate to density,
, relate to density, 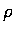 ,
as
,
as
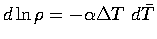 .
With
.
With
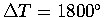 K for the non-adiabatic mantle gradient and
K for the non-adiabatic mantle gradient and
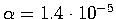 K
K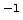 , we scale with
, we scale with
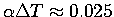 .
.
All quantitative measures used to characterize and compare different
mantle models are explained in the G-Cubed article .


Next: 3. Power spectra plots
Up: 2. Models
Previous: 2.3 Mean tomography models
(C) Thorsten Becker, USC Geodynamics, Los Angeles CA, USA, last updated 2002-01-14