

Next: 2.3 Mean tomography models
Up: 2. Models
Previous: 2.1 -wave tomography
2.2 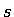 -wave tomography
-wave tomography
- grand:
- equal-area block model as of Grand's
ftp-site in fall 2000 [see Grand et al., 1997], distributed on a
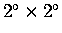 grid. The model was derived from a
combination of body and surface wave measurements with a two step
process [ Grand, 1994]: first, observations are explained in terms
of upper and lowermost mantle structure only. Second, the authors
invert the residual travel-time anomalies to find velocity
heterogeneities in the rest of the mantle.
grid. The model was derived from a
combination of body and surface wave measurements with a two step
process [ Grand, 1994]: first, observations are explained in terms
of upper and lowermost mantle structure only. Second, the authors
invert the residual travel-time anomalies to find velocity
heterogeneities in the rest of the mantle.
- ngrand:
- Updated version of grand,
as of Grand's ftp-site in June 2001. The inversion that led to
ngrand was damped more strongly in the upper mantle
than that of grand (S. Grand, pers. comm.);
as a result, the new model is different from grand mostly
in amplitude, rather than pattern, of heterogeneity (see
the G-Cubed article ).
- s20rts:
- Caltech model S20RTS, parameterized
horizontally in terms of spherical harmonics up to degree
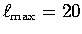 , and radially with a set of cubic splines
[ Ritsema and van Heijst, 2000]. Derived from a data set that, in addition to body
and Rayleigh wave measurements, includes observations of normal
mode splitting functions.
, and radially with a set of cubic splines
[ Ritsema and van Heijst, 2000]. Derived from a data set that, in addition to body
and Rayleigh wave measurements, includes observations of normal
mode splitting functions.
- saw24b16:
- Berkeley
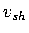 model SAW24B16
[ Mégnin and Romanowicz, 2000], derived by fitting body and surface
wave transverse-component waveforms. Parameterized with
spherical harmonics (
model SAW24B16
[ Mégnin and Romanowicz, 2000], derived by fitting body and surface
wave transverse-component waveforms. Parameterized with
spherical harmonics (
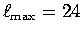 ) and cubic splines.
) and cubic splines.
- sb4l18:
- Scripps model SB4L18,
from observations of body, Love, and Rayleigh waves, and normal modes
[ Masters et al., 1999]. Parameterized in terms of equal-area blocks
(
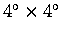 at the equator) with 18
radial layers.
at the equator) with 18
radial layers.
- s20a:
- Harvard model S20A from observations of body,
Love, and Rayleigh waves [ Ekström and Dziewonski, 1998].
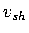 and
and 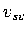 anomalies were treated as independent free parameters;
anomalies were treated as independent free parameters; 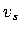 is
subsequently estimated from their Voigt average. Spherical harmonics
(
is
subsequently estimated from their Voigt average. Spherical harmonics
(
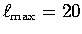 ) horizontally; radially, upper and
lower mantle are parameterized separately with two sets of
Chebyshev polynomials.
) horizontally; radially, upper and
lower mantle are parameterized separately with two sets of
Chebyshev polynomials.
- s362d1:
- Harvard model S362D1, derived with a
procedure analogous to s20a (including the
discontinuity at 660-km) but described by a cubic spline
parameterization both horizontally and vertically [ Gu et al., 2001].
Lateral resolution is equivalent to
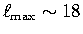 .
.
In addition, we will also use lower resolution joint inversions
for 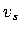 and
and 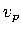 . We consider MK12WM13
[ Su and Dziewonski, 1997] (spherical harmonics,
. We consider MK12WM13
[ Su and Dziewonski, 1997] (spherical harmonics,
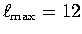 ,
Chebyshev polynomials with depth,
,
Chebyshev polynomials with depth, 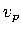 and
and 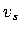 anomalies denoted by
mk12wm13p and mk12wm13s, respectively),
SB10L18 by Masters et al. [2000] (similar to sb4l18
but 10
anomalies denoted by
mk12wm13p and mk12wm13s, respectively),
SB10L18 by Masters et al. [2000] (similar to sb4l18
but 10
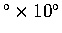 blocks, pb10l18 and
sb10l18), and Harvard model SPRD6 from normal mode splitting
coefficients [ Ishii and Tromp, 2001] (spherical harmonics,
blocks, pb10l18 and
sb10l18), and Harvard model SPRD6 from normal mode splitting
coefficients [ Ishii and Tromp, 2001] (spherical harmonics,
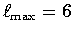 , sprd6p and sprd6s).
, sprd6p and sprd6s).


Next: 2.3 Mean tomography models
Up: 2. Models
Previous: 2.1 -wave tomography
(C) Thorsten Becker, USC Geodynamics, Los Angeles CA, USA, last updated 2002-01-14
![]() and
and ![]() . We consider MK12WM13
[ Su and Dziewonski, 1997] (spherical harmonics,
. We consider MK12WM13
[ Su and Dziewonski, 1997] (spherical harmonics,
![]() ,
Chebyshev polynomials with depth,
,
Chebyshev polynomials with depth, ![]() and
and ![]() anomalies denoted by
mk12wm13p and mk12wm13s, respectively),
SB10L18 by Masters et al. [2000] (similar to sb4l18
but 10
anomalies denoted by
mk12wm13p and mk12wm13s, respectively),
SB10L18 by Masters et al. [2000] (similar to sb4l18
but 10
![]() blocks, pb10l18 and
sb10l18), and Harvard model SPRD6 from normal mode splitting
coefficients [ Ishii and Tromp, 2001] (spherical harmonics,
blocks, pb10l18 and
sb10l18), and Harvard model SPRD6 from normal mode splitting
coefficients [ Ishii and Tromp, 2001] (spherical harmonics,
![]() , sprd6p and sprd6s).
, sprd6p and sprd6s).