|
Thorsten Becker
The University of Texas at Austin Teaching: Thermal convection |

|
[news] [research] [team] [publications] [CV] [downloads] [contact]
teaching: UT GEOL: [GP 354], [LP 315] [TG 371], other classes
[CIDER] [C] [UNIX/GMT] [SEATREE] [visuals]
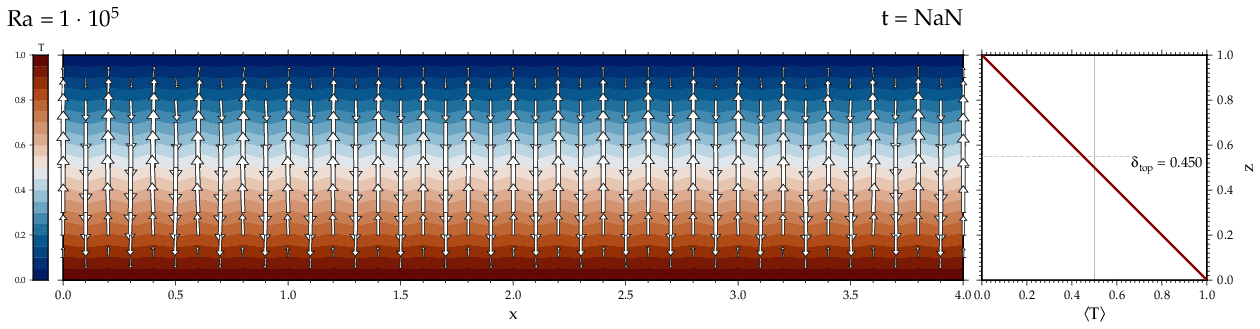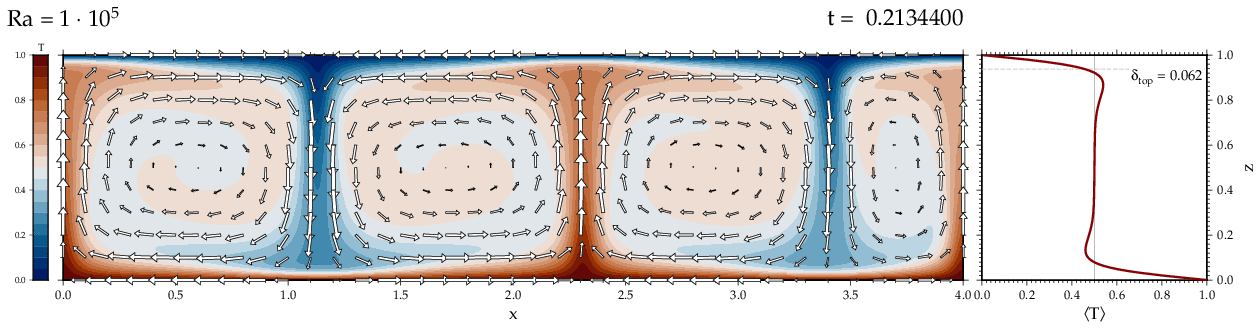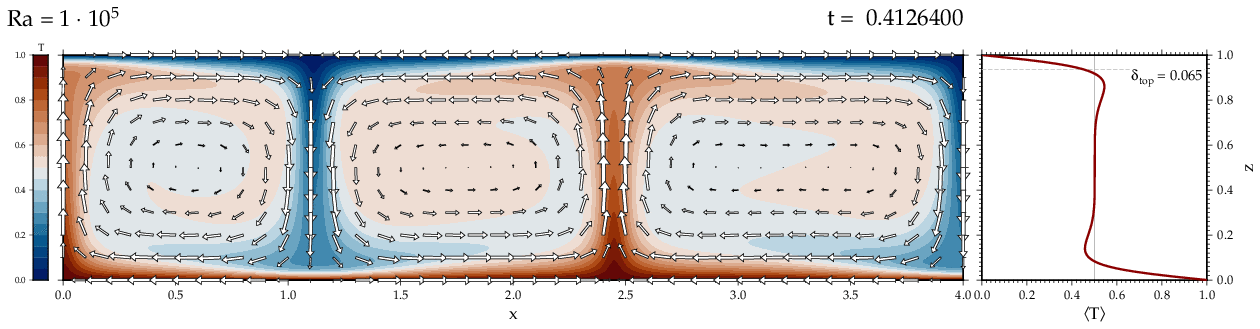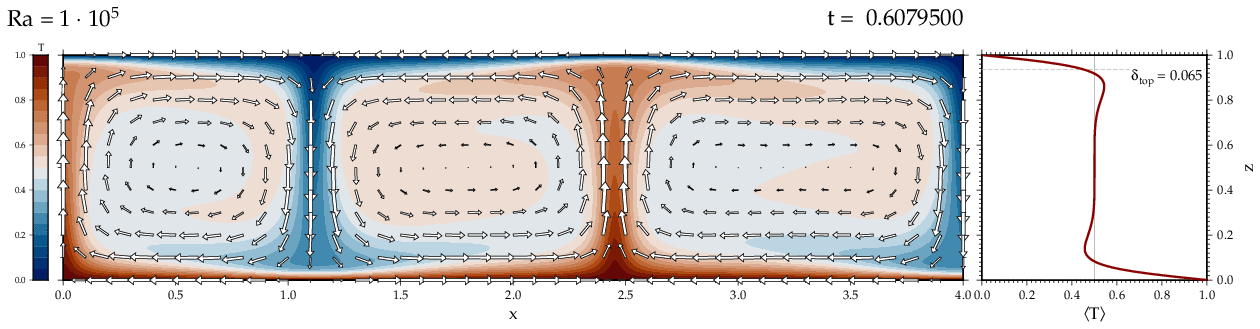
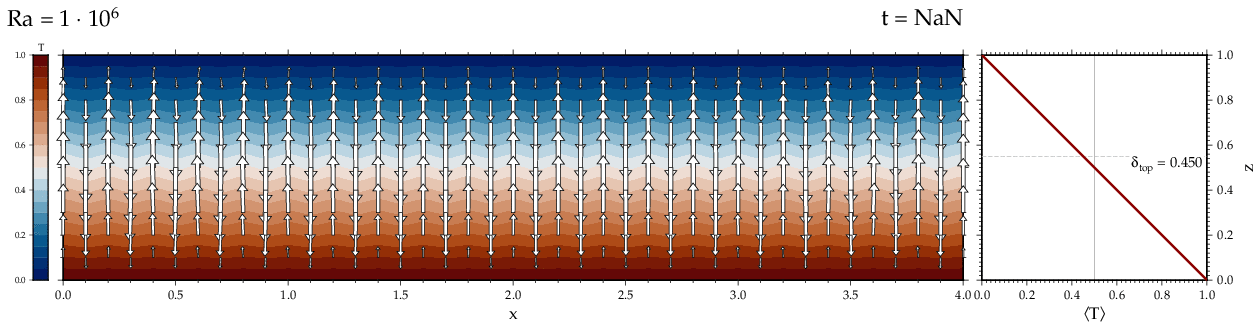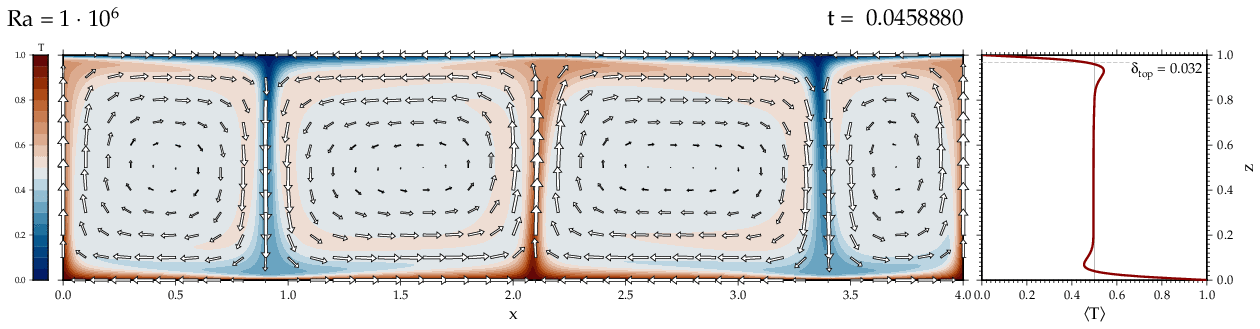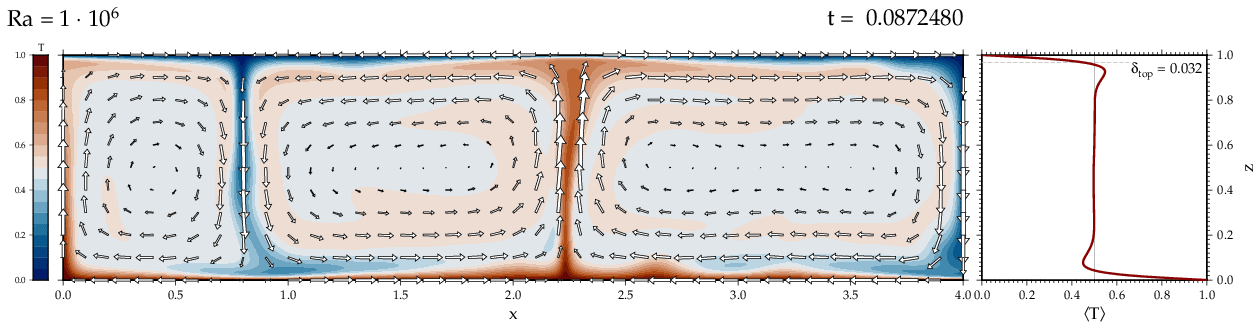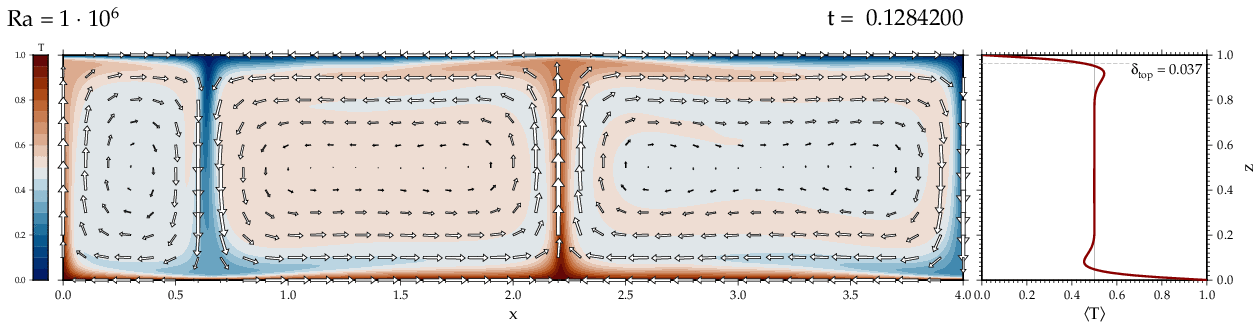
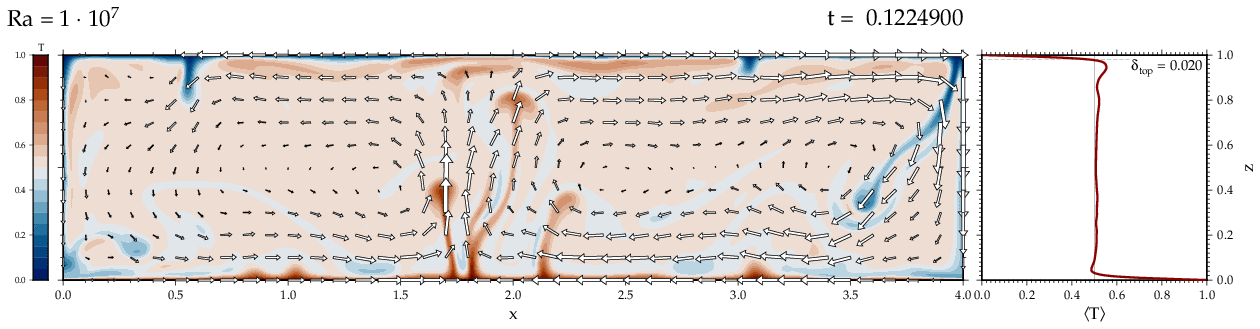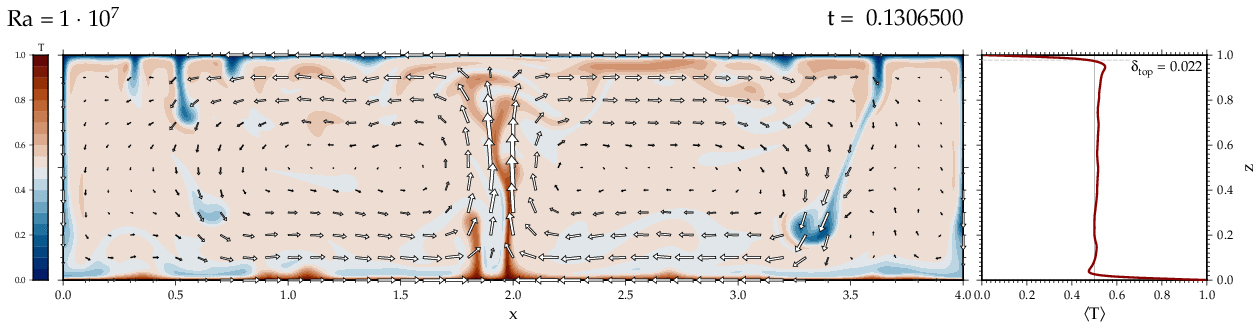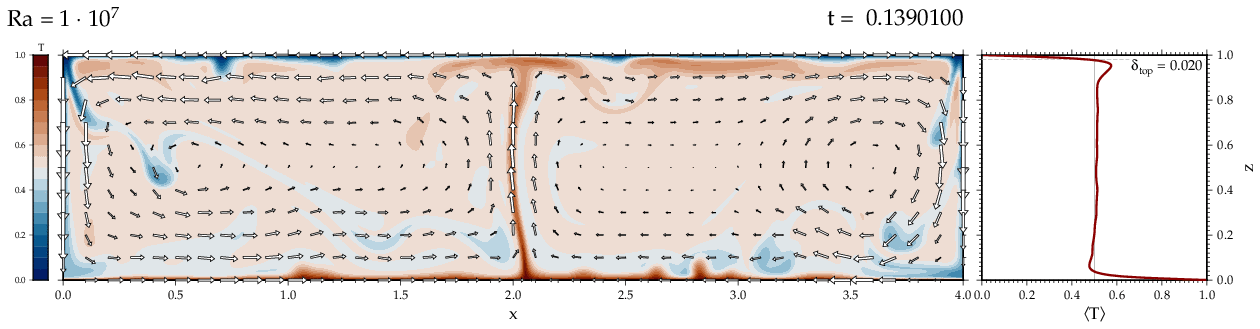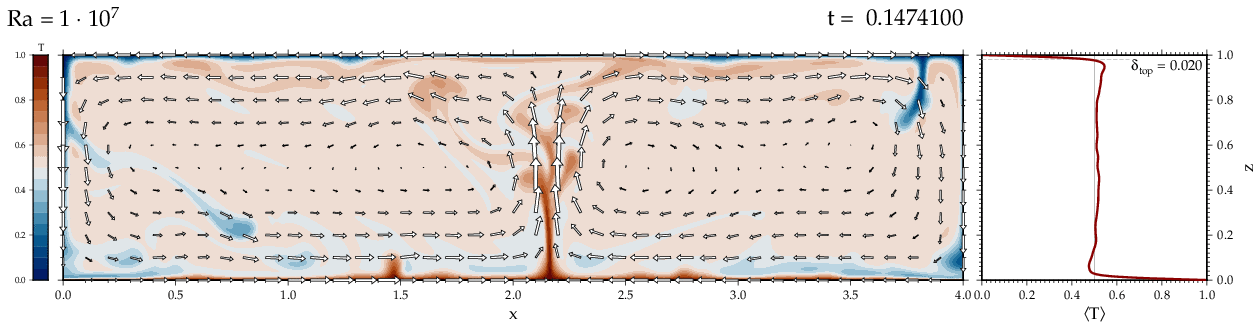
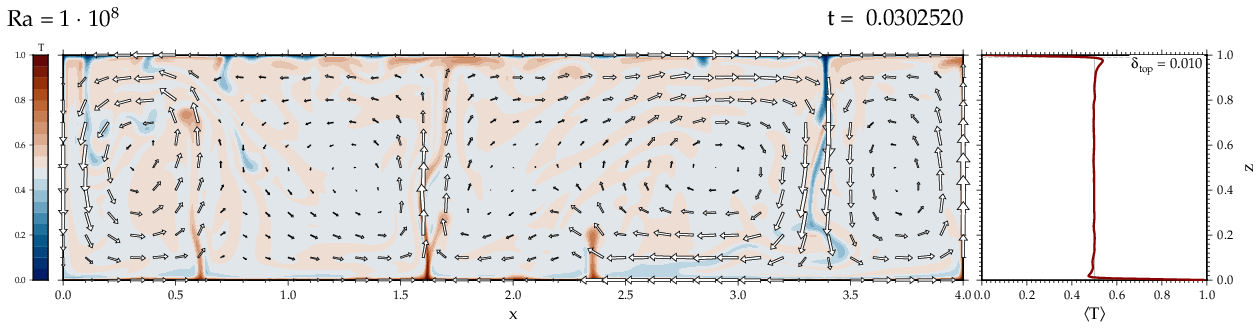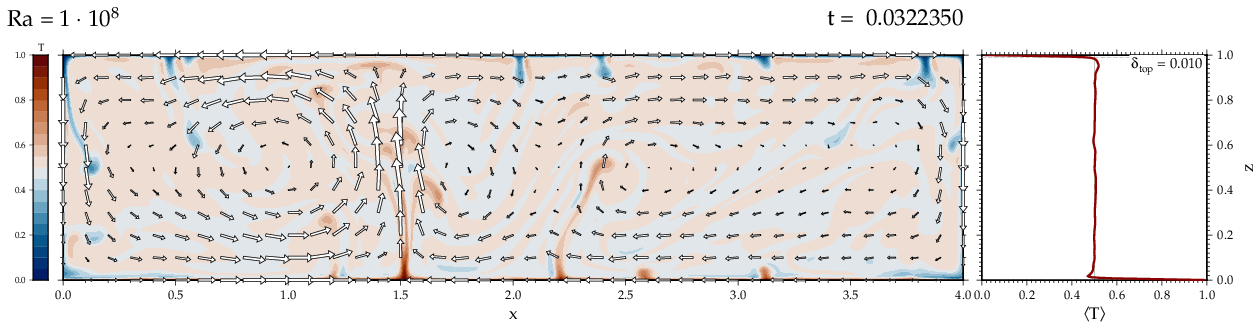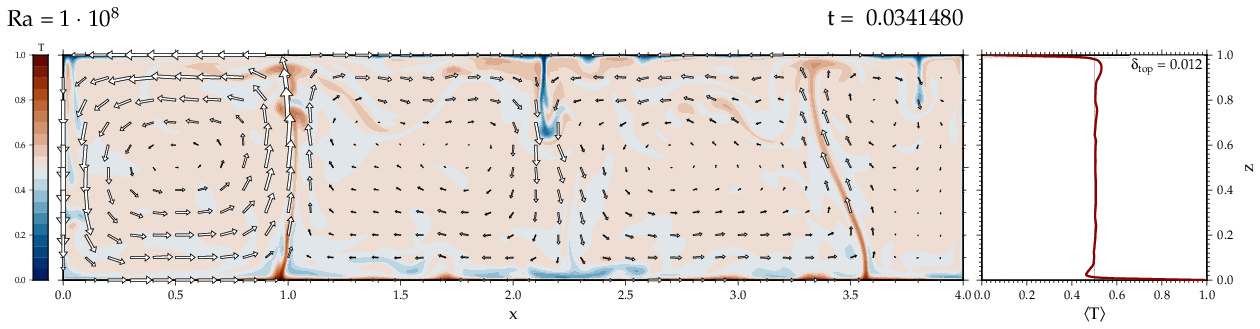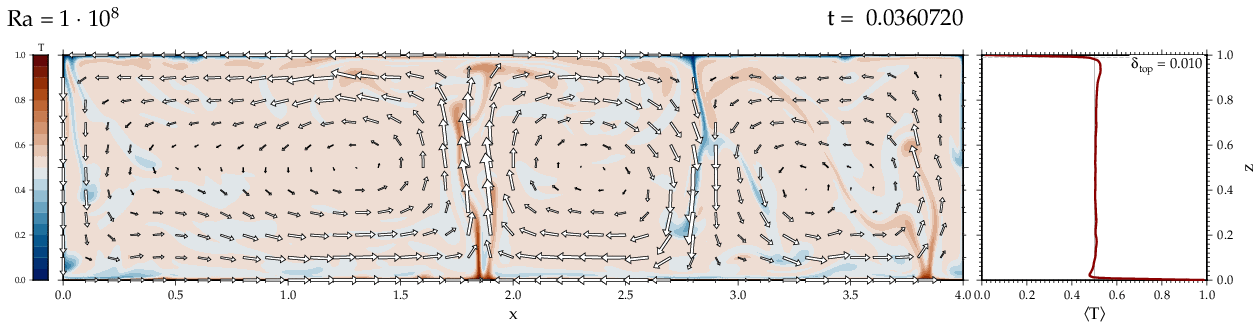
Thermal convectionThe following movies show thermal convection in the infinite Prandl number, laminar flow limit as appropriate for the Earth's mantle. The movies were produced with the finite element code Citcom by Moresi and Solomatov (1995) as modified by Allen McNamara. For discussion, see our lecture notes on Tectonic Geodynamics. Isoviscous, bottom heated modelsThe aspect ratio of the computational domain is four (4 x 1 , 2D),
there is no internal heating, fixed thermal boundary conditions on the
top and bottom (heating from below) and free slip along the
boundaries. Ra is the Rayleigh number which fully describes system
behavior for these examples. Isoviscous, mixed and internal heating models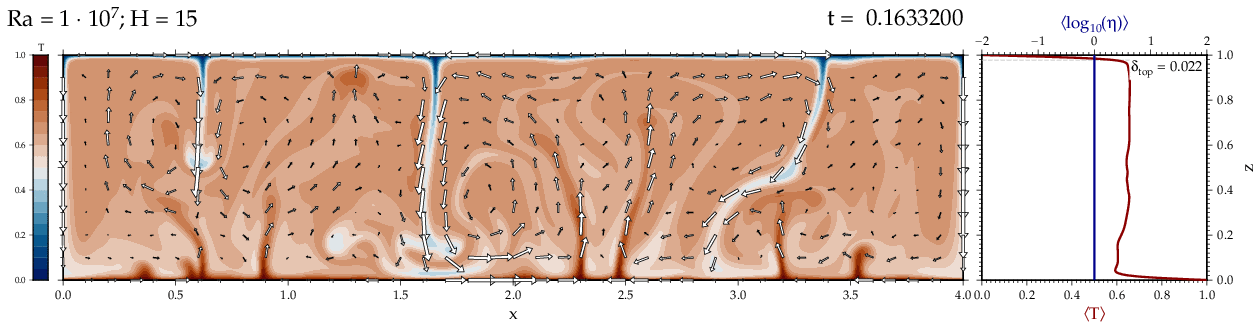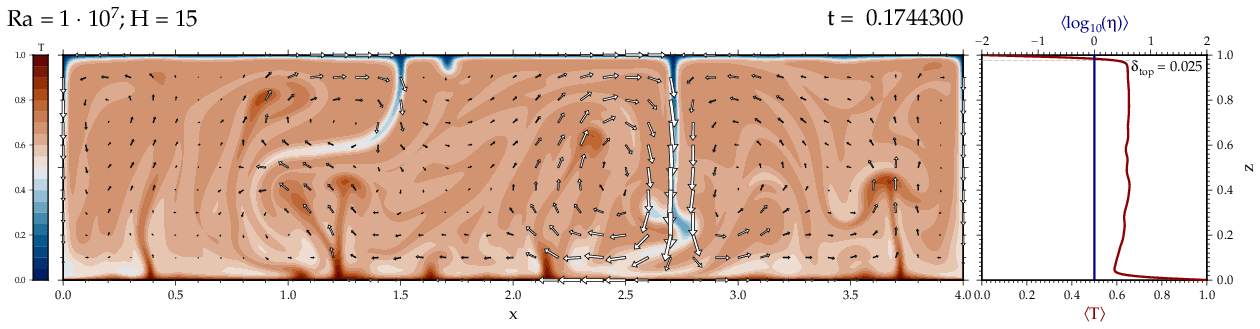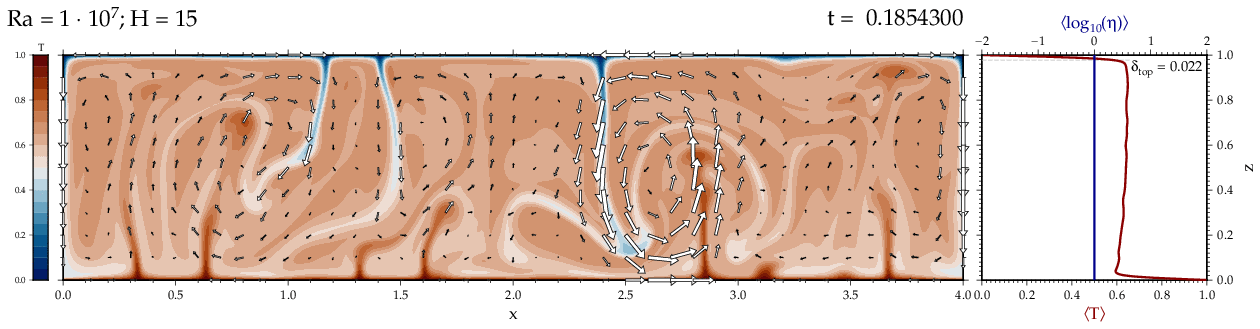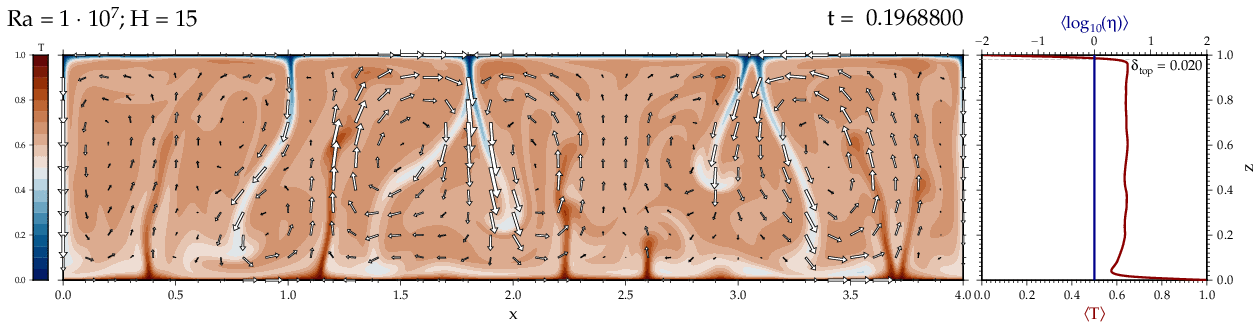  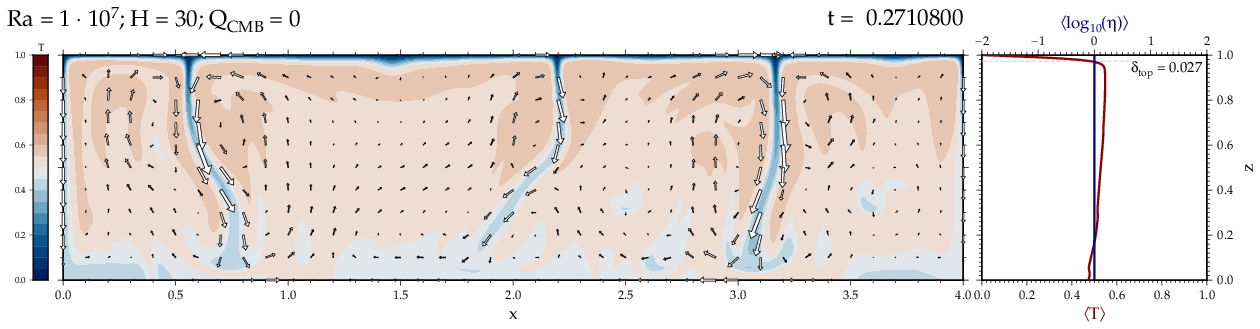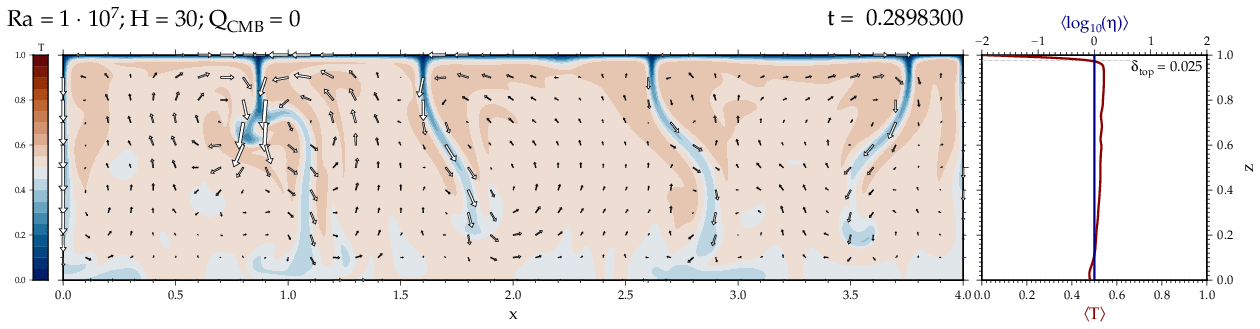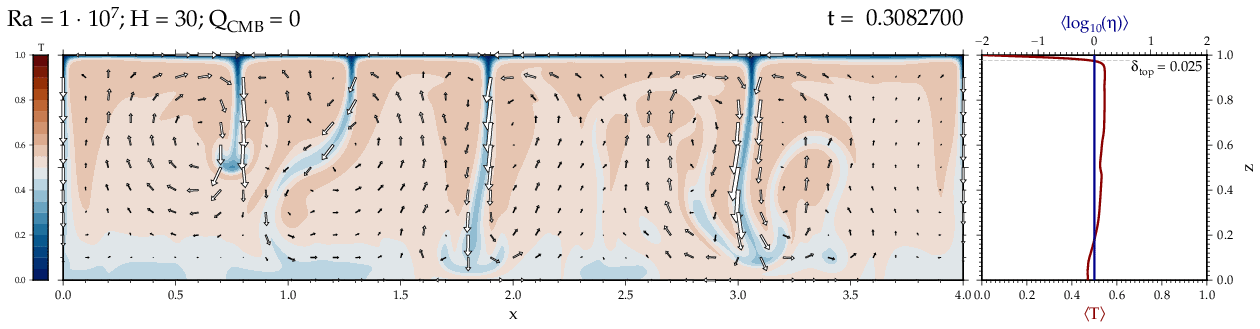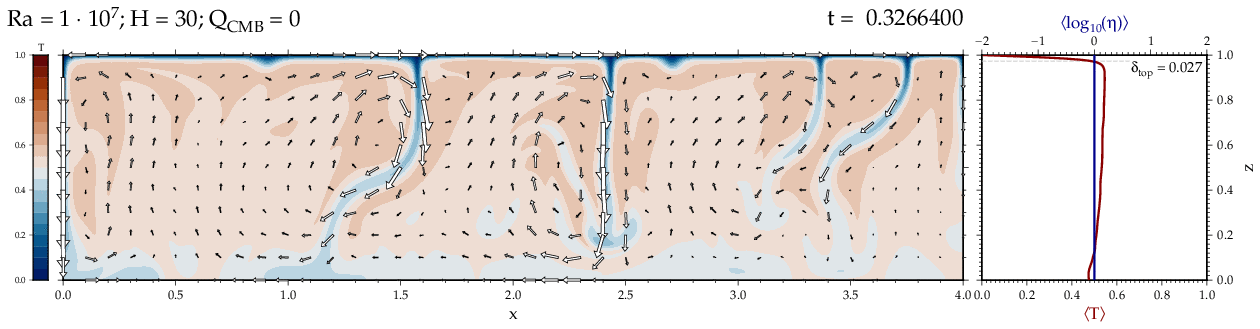 Temperature and depth-dependent viscosity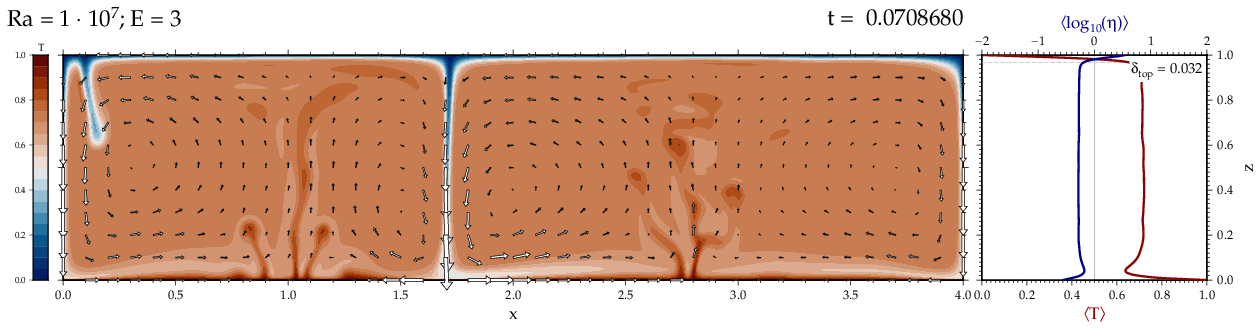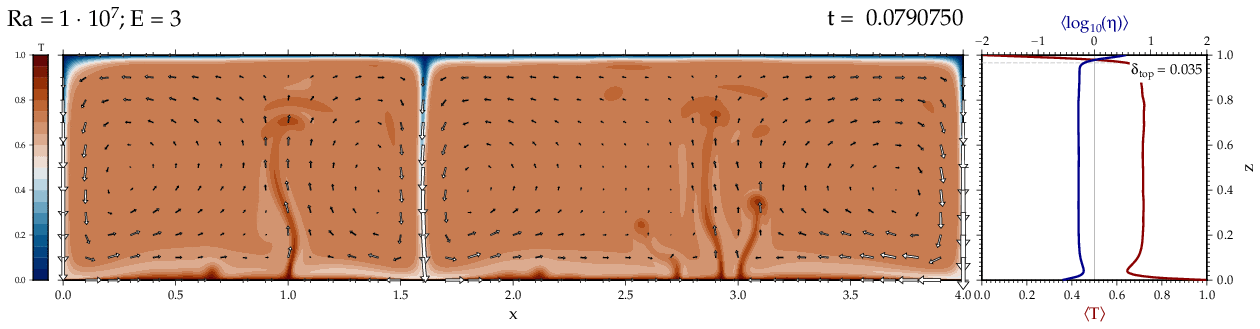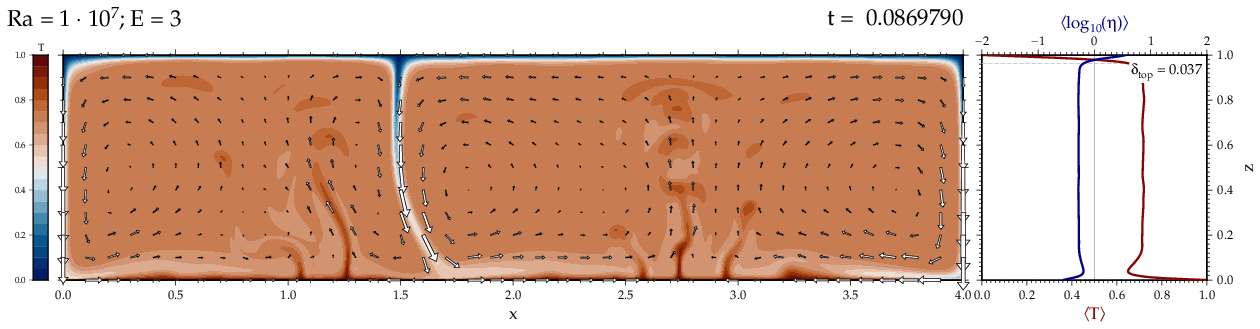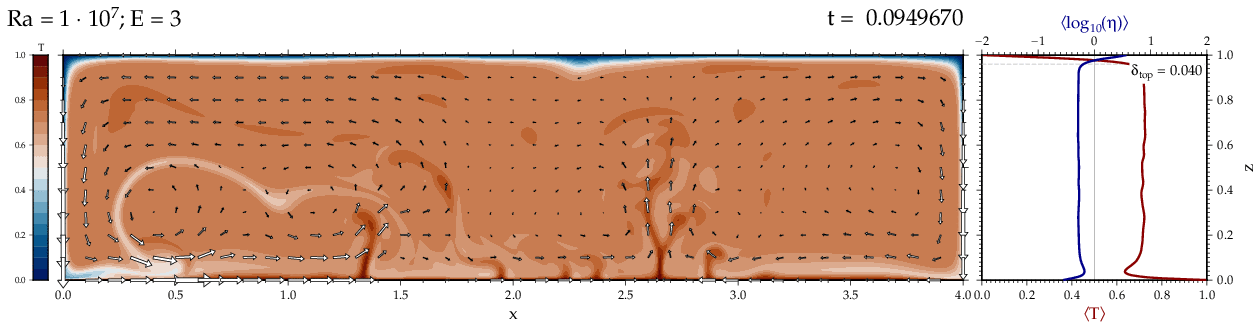 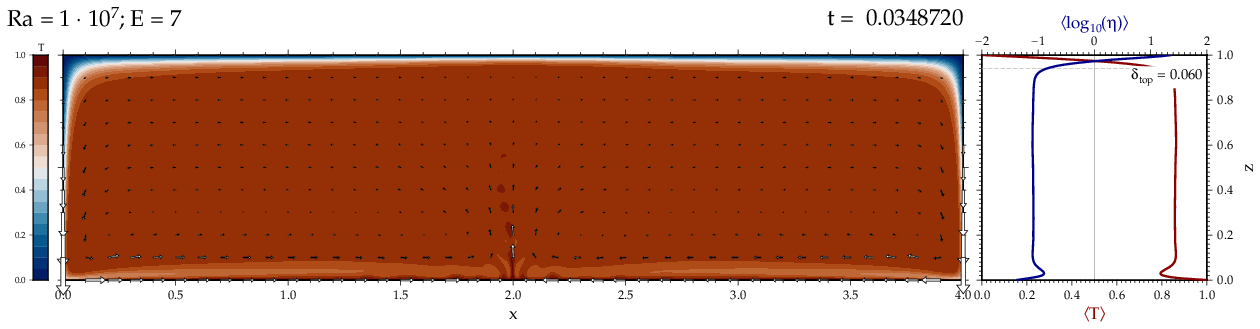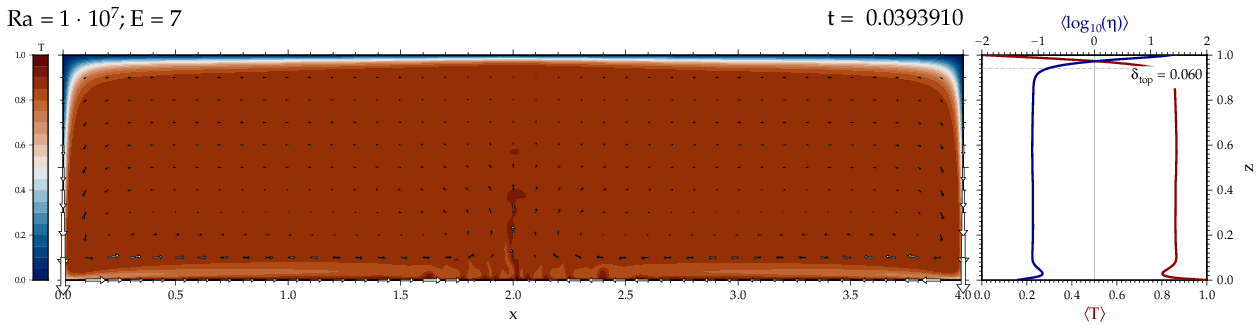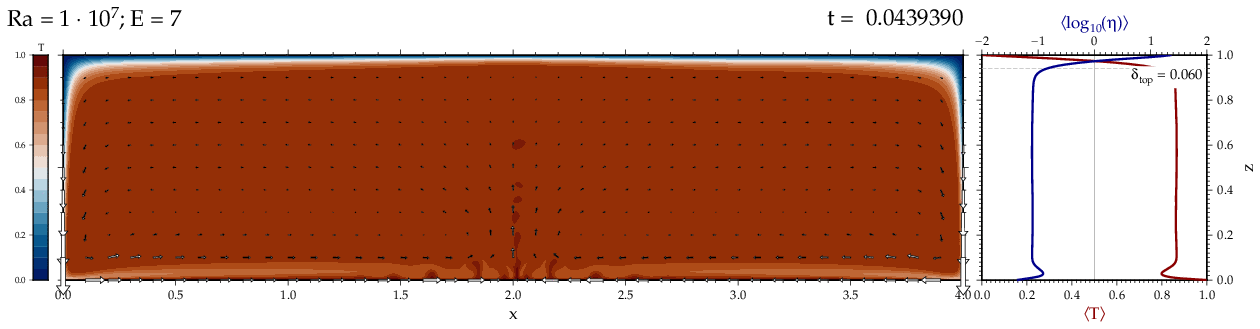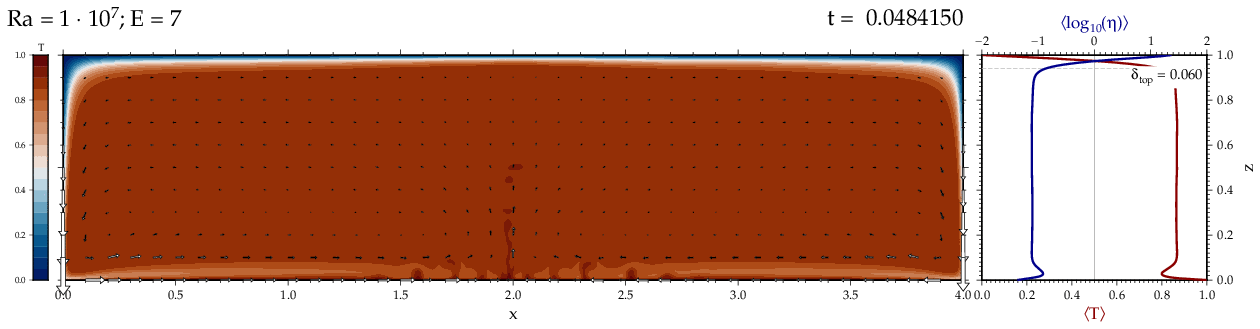 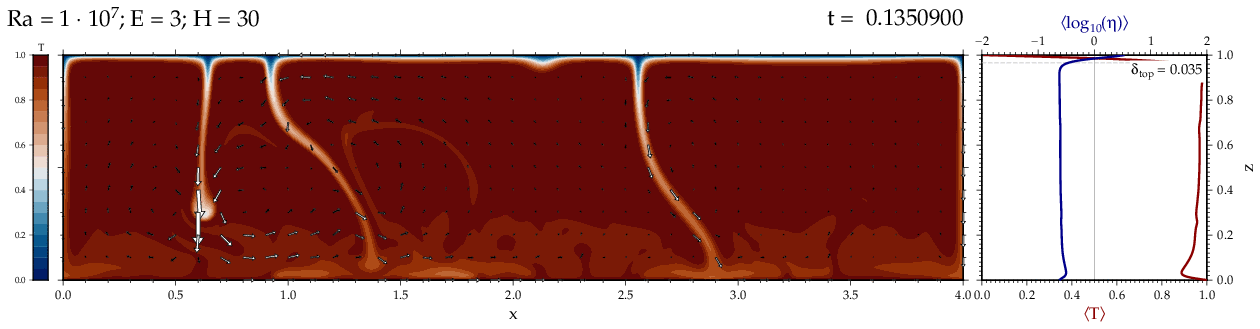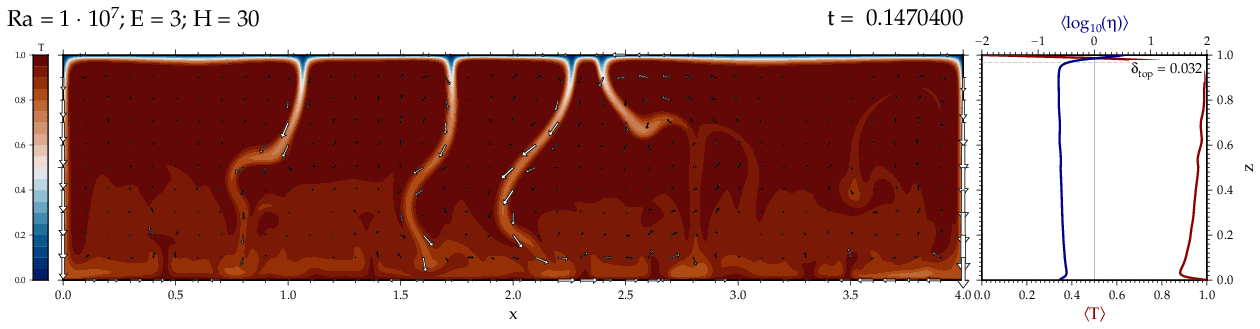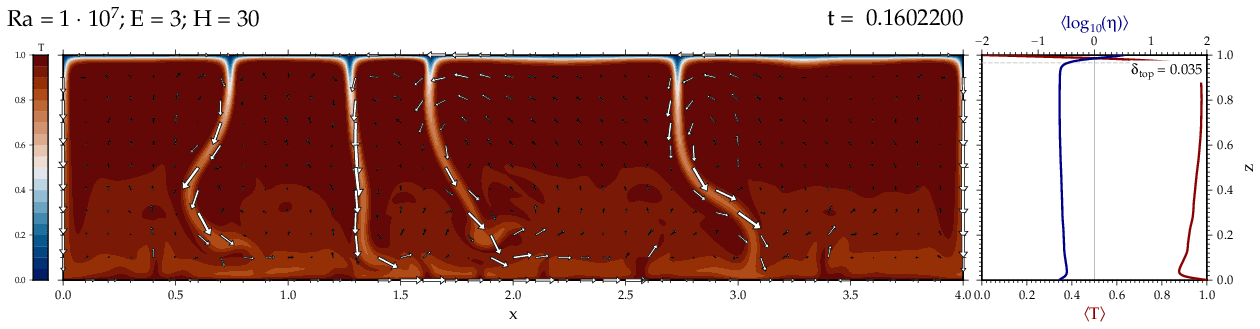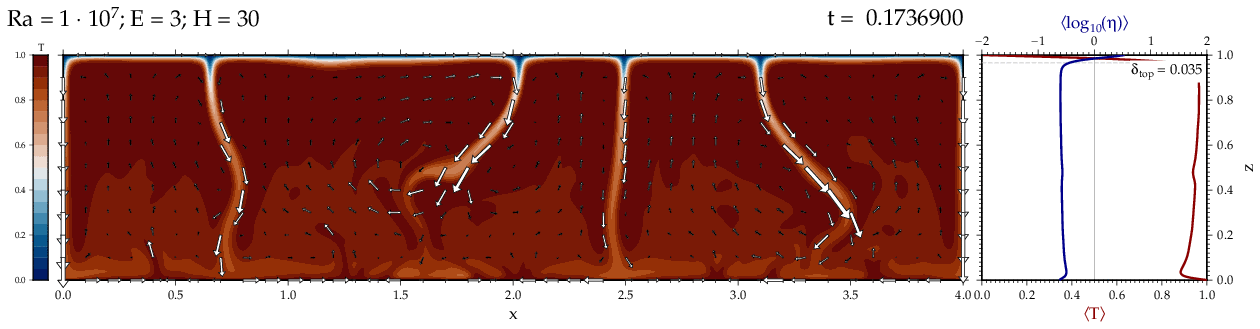 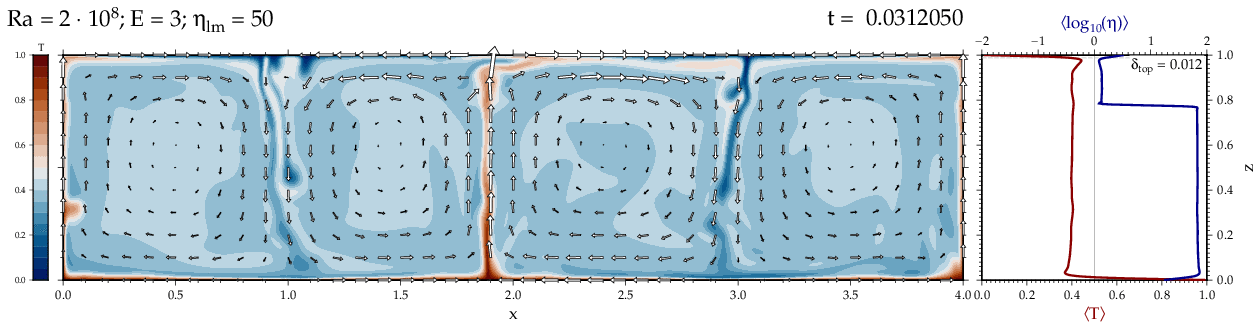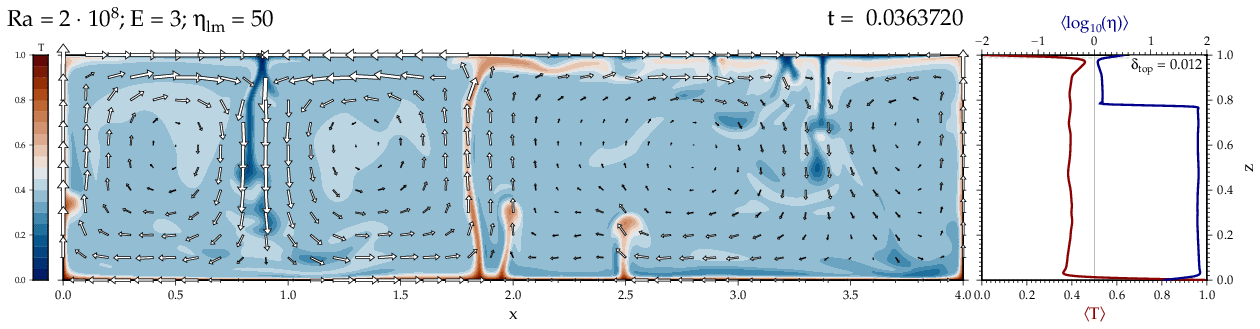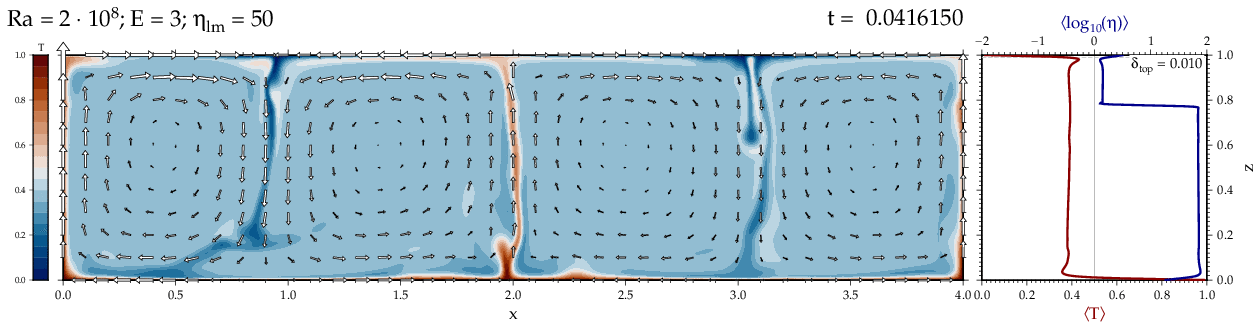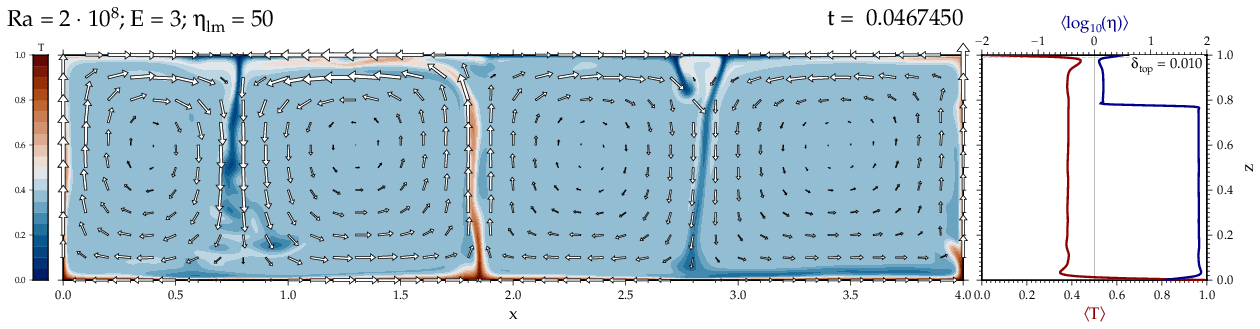  Effect of phase transitions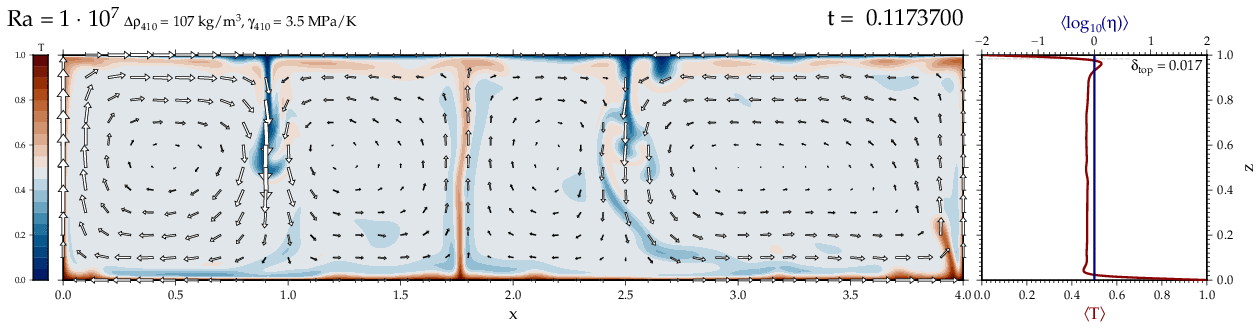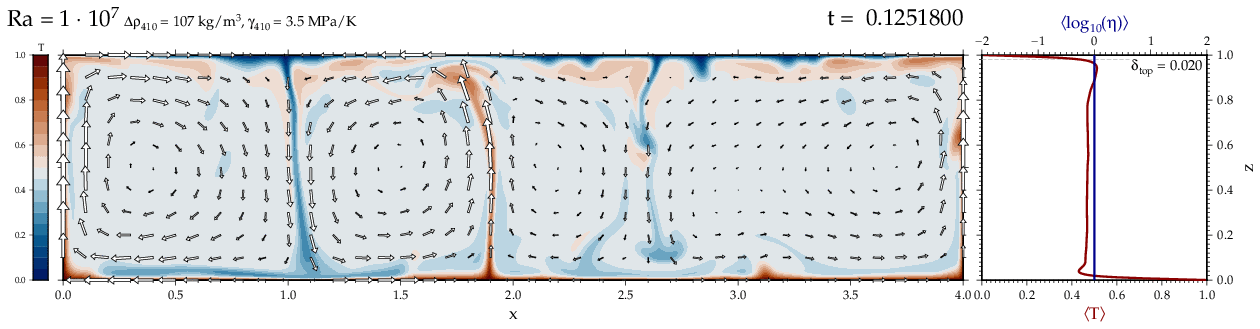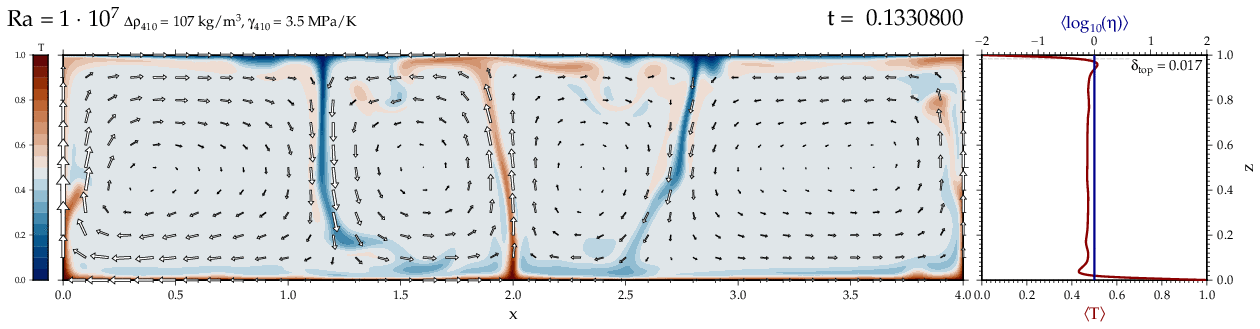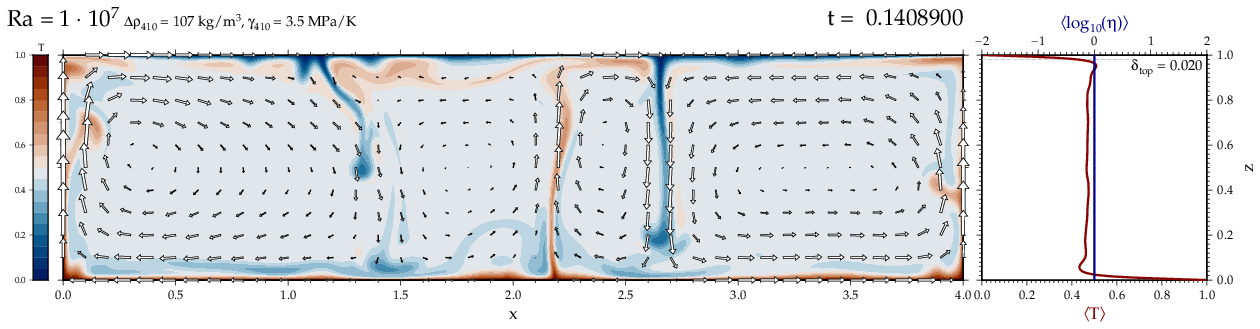 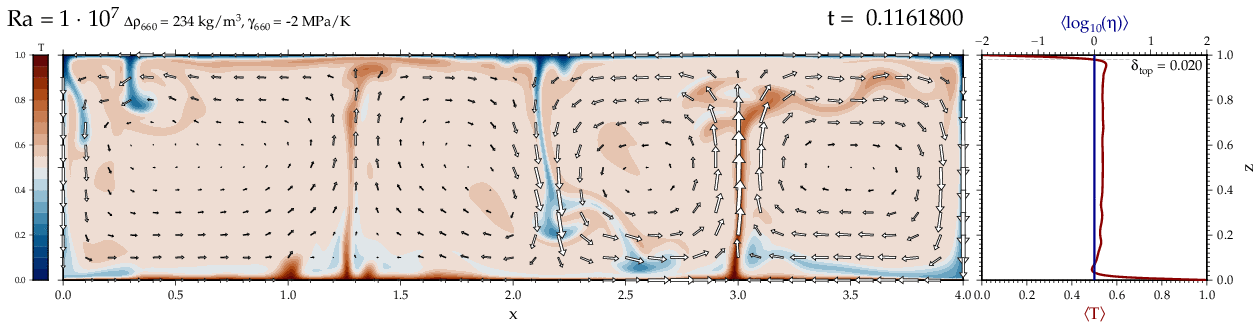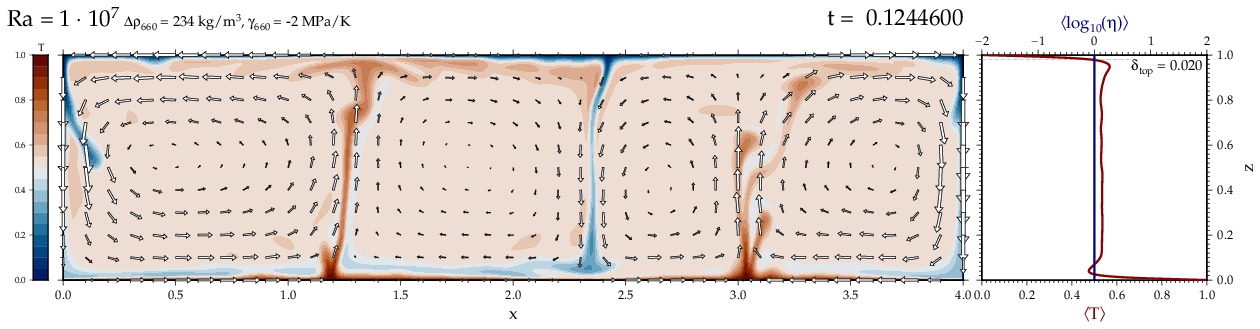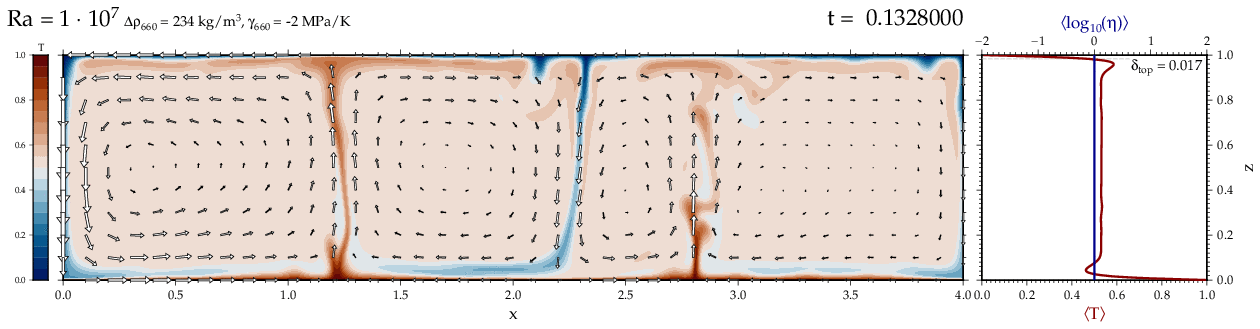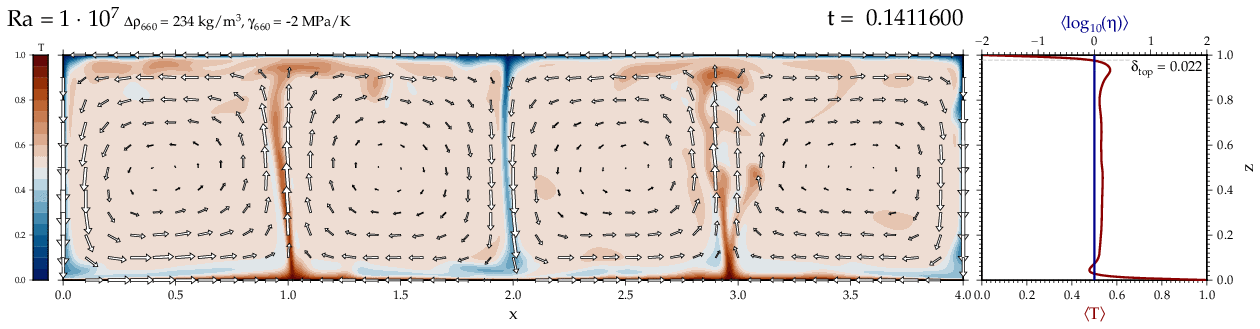  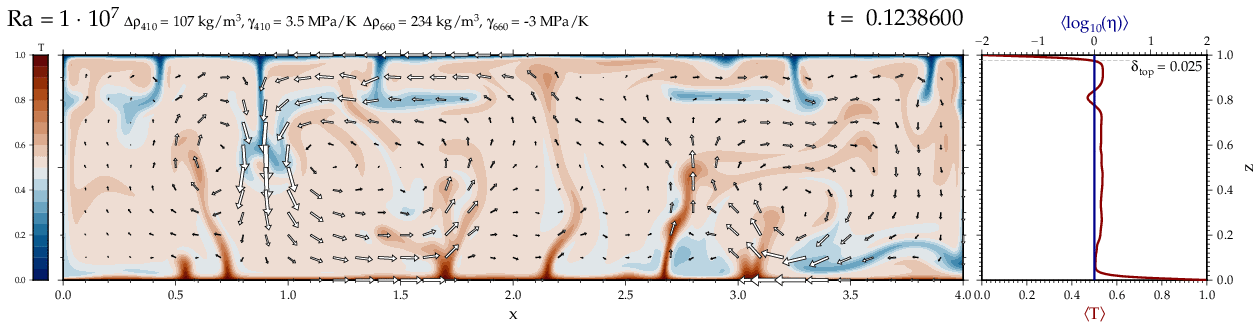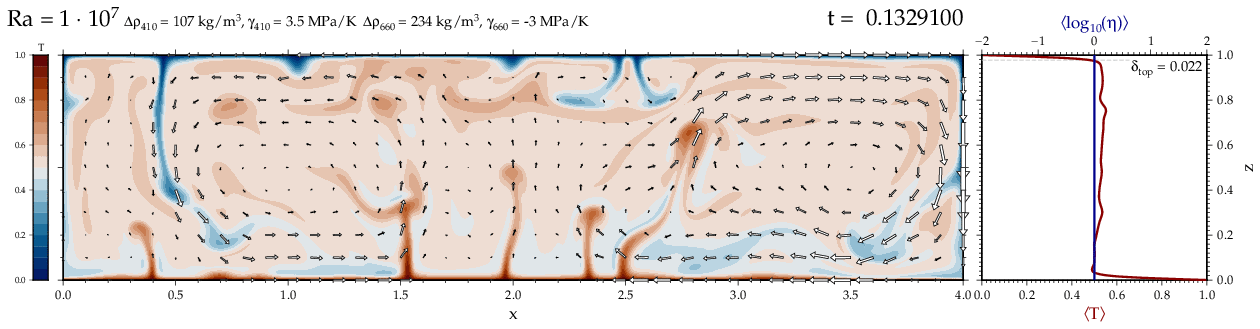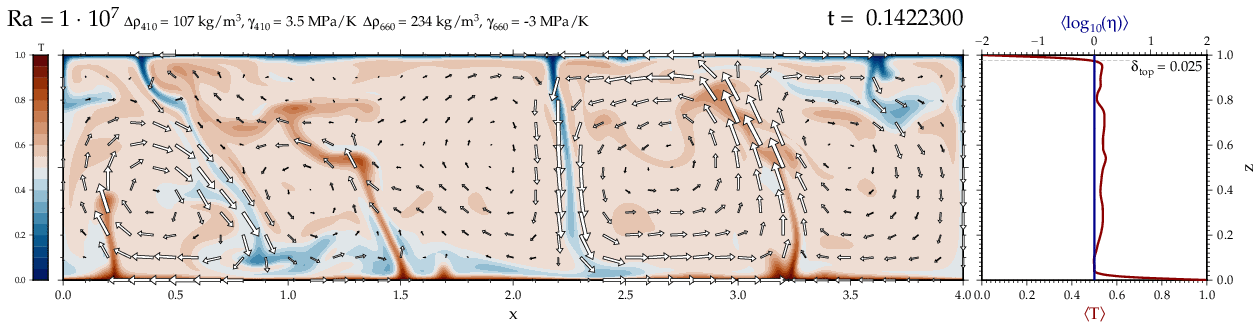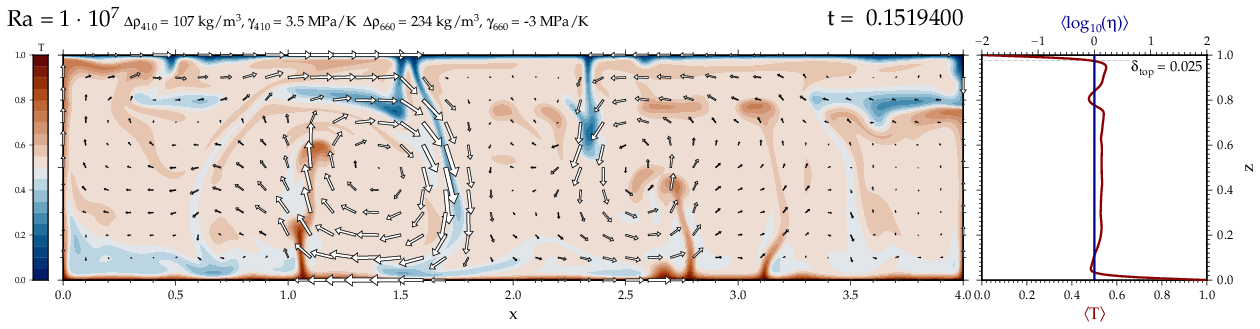  Updated: December 12, 2025 (c) Thorsten Becker, 1997-2025. |