Anisotropy model

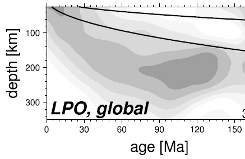
Upper mantle, seismic anisotropy from LPO and mantle flow model

1. Model I

   Best-fit model (safs417nc3_er) of Becker et al. (2008).

   • Velocity fields for the flow model

     We provide a low resolution, Netcdf/GMT grd representation of velocities of the actual flow model on which LPO computations are based in this gzipped tar file safs417nc3_er.vel.tgz. The files are v[rtp].i.grd for spherical coordinates r, theta, phi velocities (cm/yr) at i = 1, 2,...44 layers depth, sorted bottom up with depth in km given in the file vdepth.dat. The er.*grd files quantify the degree to which deformation was in the dislocation vs. diffusion creep regime (cf. Becker, 2006) and are needed to reproduce the LPO computation.

   • Horizontal projection of fast axes for azimuthal anisotropy/SKS

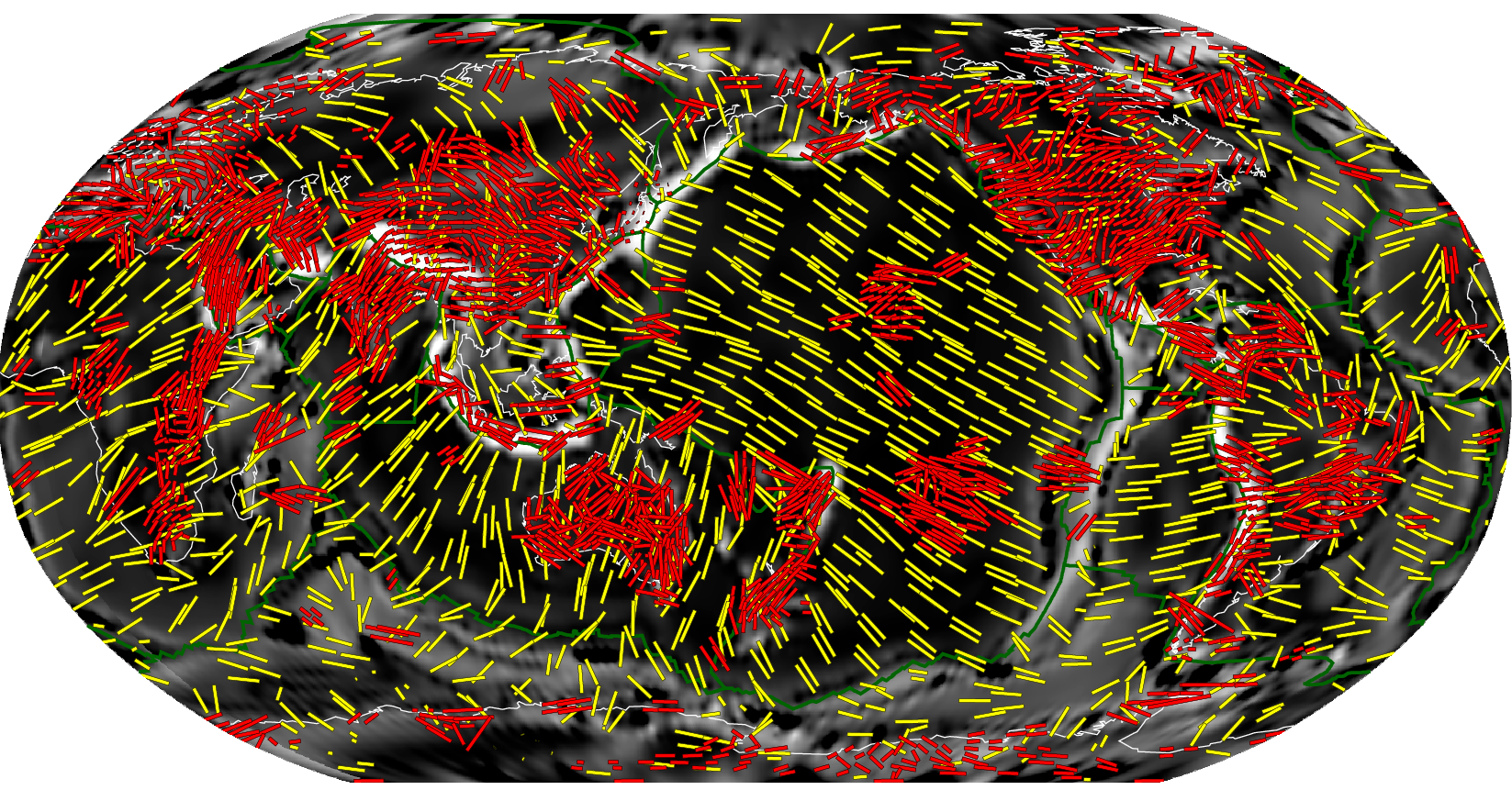     SKS splitting, for example, results from a non-linear averaging over the anisotropic elasticity tensor along the path (e.g., Becker et al., 2012). However, simplified representations can be compared with azimuthal anisotropy estimates. Here, we use the best fit hexagonal approximation of the tensor (transverse isotropy, TI, computed as in Browaeys and Chevrot, 2004), projected into the horizontal, and expressed in %.
     • Plots show this horizontal TI as yellow sticks compared to smoothed SKS splits (updated SKS splitting database from Becker et al., 2012) in red. Background shading is the radial component of the TI anisotropy. Maps of the approximate azimuthal anisotropy from the mantle flow model can be downloaded for 50, 100, 150, 200, 250, 300, and 350 km.
       
     • Model data files are given at the same depth levels:
       • tar file with LPO from Becker et al. (2008, 2014) and Auer et al. (2015) tests mantle flow model: horizontal projection of transverse isotropy axes for comparison with azimuthal anisotropy including SKS splitting
       
       Data are in format:

       lon lat azimuth(CW_from_North_degress) ...
               anisotropy_strength(%)
       

       If anisotropy strength is negative (as in a few locations), this means the slow axis is the best approximation to hexagonal anisotropy (cf. Becker et al., 2006).

   • Full anisotropic elasticity tensors

     • Model data files are given at the same depth levels as above (50, 100, ..., 350 km):
       
       • tar file with LPO from Becker et al. (2008, 2014) mantle flow model: full tensor components
       Data are in format:

       lon lat depth(km) ... 
       V_11 V_12 V_13 ... V_16 ...
       V_22 V_23 ... V_26 ...
       V_33 V_34 ... V_36 ...
       V_44 ... V46 V_55 V_56 V_66
       

       where V is the Voigt matrix representation of the elasticity tensor (in the convention of Browaeys and Chevrot, 2004, for example), given in upper triangle representation, units of GPa.

       The fstrack software package contains a number of program to process elasticity tensors in the sav format from above. For example, the best-fit TI axes were computed with sav2decompose.

   • Additional notes

     This particular LPO from flow model incorporates lateral viscosity variations in the mantle and uses dislocation/diffusion creep rheologies; it was found to match global, seismologically determined radial anisotropy averages by Becker et al. (2008), see, e.g., their Fig. 7c.

     The LPO model also matches seismologically imaged patterns of azimuthal and radial anisotropy well globally as inferred from large-scale surface-wave imaging. It can therefore in some sense be considered a reference model for the LPO-induced seismic anisotropy from mantle flow in the upper mantle (Becker et al., 2014, Auer et al., 2015), subject to further refinement.

     In particular, the flow model does not include smaller-scale density anomalies, such as underneath North America, or any intraplate plate deformation, or microplate motions, on scales smaller than the plates of the NUVEL model. This model also only captures the active mantle flow component of LPO anisotropy formation, and layers shallower than ~100 km will have little anisotropy in the model. Frozen-in anisotropy in reality may be important at those depths (Becker et al., 2008).

     The actual anisotropy is based on Kaminski et al.'s (2004) DREX method and assigning pressure and temperature dependent single crystal tensors before averaging (Becker et al., 2006), and therefore consists of the full, 21 independent elastic tensor components.

References